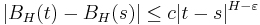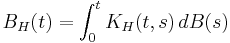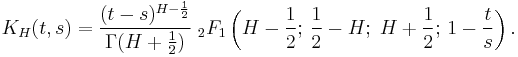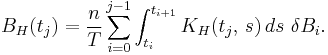Fractional Brownian motion
In probability theory, a normalized fractional Brownian motion (fBm), also called a fractal Brownian motion, is a continuous-time Gaussian process BH(t) on [0, T], which starts at zero, has expectation zero for all t in [0, T], and has the following covariance function:
where H is a real number in (0, 1), called the Hurst index or Hurst parameter associated with the fractional Brownian motion. It was introduced by Mandelbrot & van Ness (1968).
The value of H determines what kind of process the fBm is:
- if H = 1/2 then the process is in fact a Brownian motion or Wiener process;
- if H > 1/2 then the increments of the process are positively correlated;
- if H < 1/2 then the increments of the process are negatively correlated.
The increment process, X(t) = BH(t+1) − BH(t), is known as fractional Gaussian noise.
Contents |
Background and definition
Prior to the introduction of the fractional Brownian motion, Lévy (1953) used the Riemann–Liouville fractional integral to define the process
where integration is with respect to the white noise measure dB(s). This integral turns out to be ill-suited to applications of fractional Brownian motion because of its over-emphasis of the origin (Mandelbrot & van Ness 1968, p. 424).
The idea instead is to use a different fractional integral of white noise to define the process: the Weyl integral
for t > 0 (and similarly for t < 0).
Properties
Self-similarity
The process is self-similar, since in terms of probability distributions:
Fractional Brownian motion is the only self-similar Gaussian process.
Stationary increments
It has stationary increments:
Long-range dependence
For H > ½ the process exhibits long-range dependence,
Regularity
Sample-paths are almost nowhere differentiable. However, almost-all trajectories are Hölder continuous of any order strictly less than H: for each such trajectory, there exists a constant c such that
for every ε > 0.
Dimension
With probability 1, the graph of BH(t) has both Hausdorff dimension and box dimension of 2−H.
Integration
As for regular Brownian motion, one can define stochastic integrals with respect to fractional Brownian motion, usually called "fractional stochastic integrals". In general though, unlike integrals with respect to regular Brownian motion, fractional stochastic integrals are not Semimartingales.
Sample paths
Practical computer realisations of an fBm can be generated, although they are only a finite approximation. The sample paths chosen can be thought of as showing discrete sampled points on an fBm process. Three realisations are shown below, each with 1000 points of an fBm with Hurst parameter 0.75.
| H = 0.75 realisation 1 | H = 0.75 realisation 2 | H = 0.75 realisation 3 |
Two realisations are shown below, each showing 1000 points of an fBm, the first with Hurst parameter 0.95 and the second with Hurst parameter 0.55.
| H = 0.95 | H = 0.55 |
Method 1 of simulation
One can simulate sample-paths of an fBm as any Gaussian process of known covariance. Suppose we want to simulate the values of the fBM at times 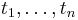 .
.
- Form the matrix
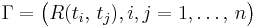 where
where 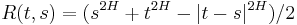 .
.
- Compute
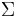 the square root matrix of
the square root matrix of 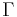 , i.e.
, i.e. 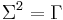 . Loosely speaking,
. Loosely speaking, 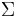 is the "standard deviation" matrix associated to the variance-covariance matrix
is the "standard deviation" matrix associated to the variance-covariance matrix 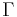 .
.
- Construct a vector
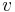 of n numbers drawn according a standard Gaussian distribution,
of n numbers drawn according a standard Gaussian distribution,
- If we define
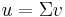 then
then 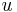 yields a sample path of an fBm.
yields a sample path of an fBm.
In order to compute 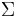 , we can use for instance the Cholesky decomposition method. An alternative method uses the eigenvalues of
, we can use for instance the Cholesky decomposition method. An alternative method uses the eigenvalues of 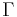 :
:
- Since
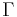 is symmetric, positive-definite matrix, it follows that all eigenvalues
is symmetric, positive-definite matrix, it follows that all eigenvalues 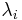 of
of 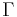 satisfy
satisfy 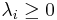 , (
, (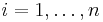 ).
).
- Let
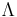 be the diagonal matrix of the eigenvalues, i.e.
be the diagonal matrix of the eigenvalues, i.e. 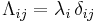 where
where 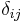 is the Kronecker delta. We define
is the Kronecker delta. We define 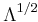 as the diagonal matrix with entries
as the diagonal matrix with entries 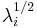 , i.e.
, i.e. 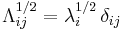 .
.
Note that this makes sense because 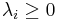 .
.
- Let
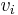 an eigenvector associated to the eigenvalue
an eigenvector associated to the eigenvalue 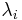 . Define
. Define 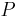 as the matrix whose
as the matrix whose  -th column is the eigenvector
-th column is the eigenvector 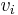 .
.
Note that since the eigenvectors are linearly independent, the matrix 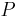 is inversible.
is inversible.
- It follows then that
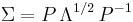 because
because 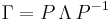 .
.
Method 2 of simulation
It is also known that
where B is a standard Brownian motion and
Where 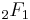 is the Euler hypergeometric integral.
is the Euler hypergeometric integral.
Say we want simulate an fBm at points 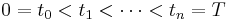 .
.
- Construct a vector of n numbers drawn according a standard Gaussian distribution.
- Multiply it component-wise by √(T/n) to obtain the increments of a Brownian motion on [0, T]. Denote this vector by
 .
.
- For each
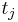 , compute
, compute
The integral may be efficiently computed by Gaussian quadrature. Hypergeometric functions are part of the GNU scientific library.
See also
- Brownian surface
- Autoregressive fractionally integrated moving average
- Multifractal: The generalized framework of fractional Brownian motions.
- Pink noise
References
- Beran, J. (1994), Statistics for Long-Memory Processes, Chapman & Hall, ISBN 0-412-04901-5.
- Lévy, P. (1953), Random functions: General theory with special references to Laplacian random functions, University of California Publications in Statistics, 1, pp. 331–390.
- Mandelbrot, B.; van Ness, J.W. (1968), "Fractional Brownian motions, fractional noises and applications", SIAM Review 10 (4): 422–437, JSTOR 2027184.
- Samorodnitsky G., Taqqu M.S. (1994), Stable Non-Gaussian Random Processes, Chapter 7: "Self-similar processes" (Chapman & Hall).
![E[B_H(t) B_H (s)]=\frac{1}{2} (|t|^{2H}%2B|s|^{2H}-|t-s|^{2H}),](/2012-wikipedia_en_all_nopic_01_2012/I/9df1180d818e9f2ede6777a13233d692.png)
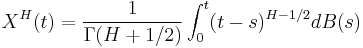
![B_H (t) = B_H (0) %2B \frac{1}{\Gamma(H%2B1/2)}\left\{\int_{-\infty}^0\left[(t-s)^{H-1/2}-(-s)^{H-1/2}\right]\,dB(s) %2B \int_0^t (t-s)^{H-1/2}\,dB(s)\right\}](/2012-wikipedia_en_all_nopic_01_2012/I/2b56d2d63e30be61ab3cc9924e18e441.png)
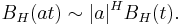
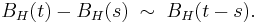
![\sum_{n=1}^\infty E[B_H (1)(B_H (n%2B1)-B_H (n))] = \infty.](/2012-wikipedia_en_all_nopic_01_2012/I/898a34a007a942a660166ebf5b9ef378.png)